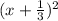Answer:
 is to be added to make
is to be added to make
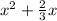 a perfect square trinomial as
a perfect square trinomial as
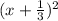
Explanation:
Given :
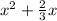
We have to find what can be added to
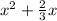 to form a perfect square trinomial.
to form a perfect square trinomial.
Perfect square trinomial is of the form
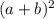
Consider the given expression
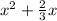
Using algebraic identity
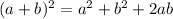 ,
,
Comparing , we get, a = x ......(1)
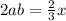
Uisng (1) , we get,
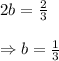
To make it a perfect square trinomial we need to add
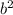 term
term

Thus,
 is to be added to make
is to be added to make
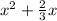 a perfect square trinomial as
a perfect square trinomial as