Answer:
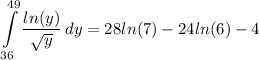
General Formulas and Concepts:
Algebra I
- Exponential Rule [Rewrite]:
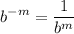
- Exponential Rule [Root Rewrite]:
![\displaystyle \sqrt[n]{x} = x^{(1)/(n)}](https://img.qammunity.org/2018/formulas/mathematics/college/cn3heqoknaut0xpqhrqaii8n5d5yhp7am9.png)
Calculus
Derivatives
Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Logarithmic Derivative:
![\displaystyle (d)/(dx) [lnu] = (u')/(u)](https://img.qammunity.org/2018/formulas/mathematics/college/76m6xhadj3reg6smmk5oo7gcf631wbl19m.png)
Integrals
Integration Rule [Reverse Power Rule]:
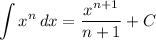
Integration Rule [Fundamental Theorem of Calculus 1]:
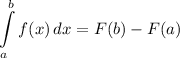
Integration Property [Multiplied Constant]:
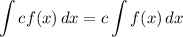
Integration by Parts:
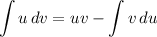
- [IBP] LIPET: Logs, inverses, Polynomials, Exponentials, Trig
Explanation:
Step 1: Define
Identify
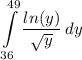
Step 2: Integrate Pt. 1
Identify and find variables for Integration by Parts.
- [LIPET] Set:
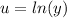
- [LIPET] Set:
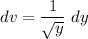
- [u] Differentiate [Logarithmic Derivative]:
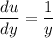
- [u] Rewrite:
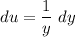
- [dv] Integrate [Integration Rule - Reverse Power Rule]:
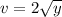
Step 3: Integrate Pt. 2
- [Integral] Integration by Parts:
![\displaystyle \int\limits^(49)_(36) {(ln(y))/(√(y))} \, dy = \bigg[ 2ln(y)√(y) \bigg] \bigg| \limits^(49)_(36) - \int\limits^(49)_(36) {(2√(y))/(y)} \, dy](https://img.qammunity.org/2018/formulas/mathematics/college/2vzu8lnr1a8nwmvgdqvjh43m74ik4kkzt1.png)
- [Integral] Simplify/Rewrite [Integration Property - Multiplied Constant]:
![\displaystyle \int\limits^(49)_(36) {(ln(y))/(√(y))} \, dy = \bigg[ 2ln(y)√(y) \bigg] \bigg| \limits^(49)_(36) - 2\int\limits^(49)_(36) {(1)/(√(y))} \, dy](https://img.qammunity.org/2018/formulas/mathematics/college/jf26vndj45z2dj2elll8myi9oosl3nsi4p.png)
- [Integral] Reverse Power Rule:
![\displaystyle \int\limits^(49)_(36) {(ln(y))/(√(y))} \, dy = \bigg[ 2ln(y)√(y) \bigg] \bigg| \limits^(49)_(36) - 2 \bigg[ 2√(y) \bigg] \bigg| \limits^(49)_(36)](https://img.qammunity.org/2018/formulas/mathematics/college/pbnzfbhyxinlj1lsg89a9l5tbvi6px1pjn.png)
- Evaluate [Integration Rule - FTC 1]:
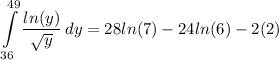
- Simplify:
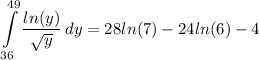
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration
Book: College Calculus 10e