Partition the interval [0,1] as
![\left[0,\frac15\right]\cup\left[\frac15,\frac25\right]\cup\left[\frac25,\frac35\right]\cup\left[\frac35,\frac45\right]\cup\left[\frac45,5\right]](https://img.qammunity.org/2018/formulas/mathematics/high-school/mnhzxb7d7146nc8dwso55iuxf257tamae5.png)
The midpoints of the intervals are, respectively
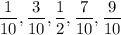
- these are your sample points.
The integral is approximated by

where
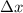
is the difference between the partition endpoints, i.e.

, and
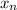
is the midpoint of the

th partition. You have
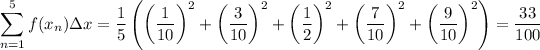
For comparison, the actual value of the integral is

, so the approximation is valid to two decimal places.