Question

A parabola whose equation is y = (x - 5)^2 - 2 has a vertex at _____.

(-5, -2)
(-5, 2)
(5, -2)
(5, 2)

Answer 1

(5, -2) because y=(x-5)^2-2 is really y=x^2-10x+23 after you foil then take the derivative which is y'=2x-10 solve for x and you get 5 then put 5 in the original equation and you get -2 so the answer is (5, -2)

Answer 2

Option 3 - (5,-2)

Explanation:

Given : A parabola whose equation is
`y=(x-5)^2-2`

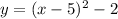
To find : The vertex of the parabola

Solution :

The general vertex form of parabola is

`y=a(x-h)^2+k`

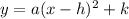
Where, (h,k) is the vertex of the function.

The given function is already in vertex form so we compare it with general form

`y=(x-5)^2-2`

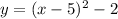
a =1, h=5 and k=-2

So, The vertex of the given parabola is (h,k)=(5,-2)

Therefore, Option 3 is correct.