Question

The cone shown has a diameter of 18 meters and a slant height of 15 meters. Which choice is closest to the lateral surface area? Use 3.14 to approximate pi.

Answer 1

Its 424 square meters

Answer 2

If you unfurl the lateral "face" of a cone, you get the sector of a circle whose central angle subtends an arc with length
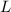
`L` equal to the circumference of the cone's base, and a radius equal to the slant height
`s` of the cone.

Since the diameter of the base is 18m, the circumference of the base is about
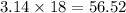
`3.14*18=56.52` meters, so this is the value of
`L`.

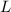
You're given a slant height of
`s=15` meters.

Now, the following proportional relation holds for any circle:


`\frac{\text{area of sector}}{\text{area of circle}}=\frac{\text{arc length of sector}}{\text{circumference of circle}}`

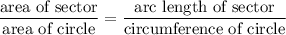
This translates to


`\frac A{\pi* s9^2}=\frac s{2\pi s*9}`

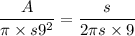
(remember, we're talking about a sector of a circle with radius
`s` and arc length
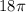
`18\pi`). Solving for
`A`:


`\frac A{81*3.14}=(15)/(18*15*3.14)`

`A=\frac92=4.5`

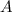
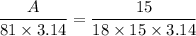
So the area of the lateral face is approximately 4.5 square meters.