If you unfurl the lateral "face" of a cone, you get the sector of a circle whose central angle subtends an arc with length
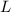
equal to the circumference of the cone's base, and a radius equal to the slant height

of the cone.
Since the diameter of the base is 18m, the circumference of the base is about
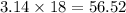
meters, so this is the value of
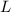
.
You're given a slant height of

meters.
Now, the following proportional relation holds for any circle:
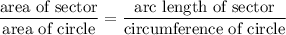
This translates to
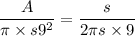
(remember, we're talking about a sector of a circle with radius

and arc length
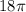
). Solving for
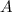
:
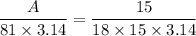
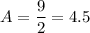
So the area of the lateral face is approximately 4.5 square meters.