Hey there :)
Sorry this took me a long time. I wrote down my answers then realized my phone didn't want to attach a picture along with it.
To solve these equations, we must first understand what the quadratic formula is.
An equation, when graphed, might have a zero, or not. Think of a parabola. If a positive parabola starts above the x-axis, there is no way there would be a solution at the x-axis, more commonly called a zero. In this case, if you solve the equation, it would end up as no solution.
Thinking of the same positive parabola, if the vertex (lower most point) would show up ON the x-axis, this would end up as one solution when solving to use a quadratic formula.
Lastly, if this same positive parabola's vertex lies under the x-axis, it will always have two solutions. A parabola is shaped like the letter 'U' and will have two ends that will at some point cross the x-axis, making it a zero.
A standard quadratic equation starts as
 , and this aligns with the quadratic formula to find a zero:
, and this aligns with the quadratic formula to find a zero:
x=(-b±
 )/2a
)/2a
Let's start off with the first problem.
Let's move the -1 to the other side to make it equal to 0. This way, we can easily use the quadratic equation to find the answer.
Adding 1 on both sides will get rid of the negative 1 and replace it with a zero.
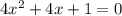
Knowing 4 is a, 4 is b, and 1 is c, let's plug it into the quadratic formula.
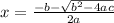 and
and
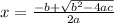
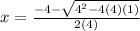 and
and
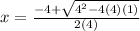
Let's solve further. Note the square root of zero is just zero.
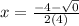 and
and
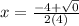
These are both the same equations since anything plus or minus 0 is just -4.
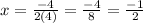
Since for this problem, we only got one solution, this quadratic formula for the first one is just one solution with the zero at (-0.5,0)
Let's solve the second one, using the same methods we did above.
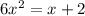
Let's move both x and 2 to the other side, because we want the quadratic equation to equal to a zero.
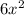 = x+2
= x+2
-x-2 -x-2
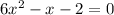
Knowing a is 6, b is NEGATIVE 1, and c is NEGATIVE 2, let's plug it in the quadratic equation.
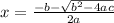 and
and
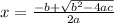
 and
and
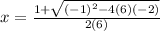
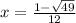 and
and

Let's keep simplifying.
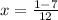 ,
,
 and
and
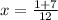 ,
,
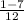
The reason why I have both -7 and 7 in both equations is that we have to be careful that the square root of 49 is 7 and -7 (since -7*-7 is still 49 as well). This equation rounded out perfectly as the same values so we ended up having two solutions, but when you're having 2 nonreal and 2 real solutions in the future, it's crucial to know this step.
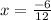 and
and
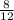
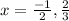
We get two solutions, which mean that there are two solutions at (
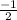 ,0) and (
,0) and (
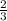 ,0)
,0)