Question

The center of mass of a cow and the center of mass of a tractor are 208 meters apart. The magnitude of the gravitational force of attraction between these two objects is calculated to be 1.8 × 10-9 newtons.

What would the magnitude of the gravitational force of attraction be between these two objects if they were 416 meters apart?
A.
1.62 × 10-9 newtons
B.
3.6 × 10-10 newtons
C.
9 × 10-10 newtons
D.
4.5 × 10-10 newtons

Answer 1

`4.5* 10^(-10)\ N`

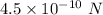
Step-by-step explanation:

The gravitational force between two masses is inversely proportional to the square of the distance between them such that,

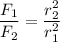`(F_1)/(F_2)=(r_2^2)/(r_1^2)` .....(1)

We have,

r₁ = 208 m,
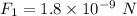`F_1=1.8* 10^(-9)\ N`, r₂ = 416 m, F₂ = ?

Put all the values in relation (1) such that,

`F_2=(F_1r_1^2)/(r_2^2)\\\\F_2=(1.8* 10^(-9)* 208^2)/(416^2)\\\\F_2=4.5* 10^(-10)\ N`

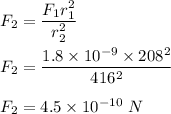
So, the required force is
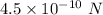`4.5* 10^(-10)\ N`. Hence, the correct option is (d).