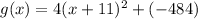Answer:
The vertex form of a quadratic function is given by
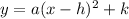 , where (h, k) is the vertex of the parabola.
, where (h, k) is the vertex of the parabola.
Given the function :
g(x) =
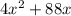
g(x) =
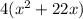
Now, we will be completing the square ;
g(x) =
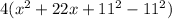 =
=
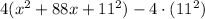
⇒ g(x) =
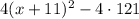 or
or
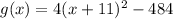
therefore, the given function is in the vertex form is,