Which expression is equivalent to the one shown below? (4z)^-3 x (2z)^5

Question

asked Aug 19, 2018 115k views

2 Answers

Loftx · Answer 1 · 2018-08-21T01:39:36+0000

Answer:

$(1)/(2)\cdot z^2$ is the required equivalent expression.

Explanation:

We have been given an expression:

$(4z)^(-3)\cdot (2z)^5$

First open the parenthesis and simplify we will get:

$(1)/(4^3\cdot z^3)\cdot 2^5\cdot z^5$

$(1)/(64z^3)\cdot 32z^5$

On simplification by dividing 64 by 32

$(1)/(2\cdot z^3)\cdot z^5$

When positive power changes its position from denominator to numerator its sign changes and vice-versa.

$(1)/(2)\cdot z^(5-3)$

$(1)/(2)\cdot z^2$ is the required equivalent expression.

Biniam · Answer 2 · 2018-08-26T04:13:04+0000

Answer:

Equivalent expression is
$(1)/(2)\cdot z^2$ .

Explanation:

Given:
(4z)^(-3) ×
(2z)^(5)

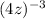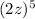
To find: Which expression is equivalent to the one shown below.

Solution: We have given that
(4z)^(-3) ×
(2z)^(5) .

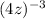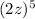By the negative exponent rule
a^(-m) =
(1)/(a^(m) ) .

(4z)^(-3) *
(2z)^(5) =

(2z)^(5) *
(1)/((4z)^(3) )

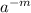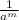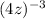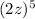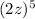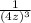
We got
(1)/((4z)^(3) ) *
(2z)^(5) .

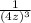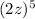On removing parenthesis

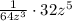$(1)/(64z^3)\cdot 32z^5$ .

On dividing 64 by 32

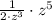$(1)/(2\cdot z^3)\cdot z^5$ .

By the quotient rule of exponent

(a^(m) )/(a^(n)) =
a^(m-n) .

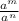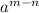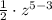$(1)/(2)\cdot z^(5-3)$ .

$(1)/(2)\cdot z^2$ .

Therefore, Equivalent expression is
$(1)/(2)\cdot z^2$ .