Answer:
the radius of Earth's orbit will become 4 times the original radius
Step-by-step explanation:
The gravitational force between the Sun and the Earth is given by:
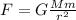
where
G is the gravitational constant
M is the mass of the Sun
m is the mass of the Earth
r is the radius of the Earth's orbit
This force provides the centripetal force that keeps the Earth in (approximately) circular motion around the Sun, therefore we can write
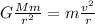
where the term on the right is the centripetal force, with v being the Earth's velocity. Re-arranging the equation, we can write r (the radius of the orbit) as a function of the velocity v:
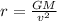
we see that the orbital radius is inversely proportional to the square of the velocity: therefore, if the velocity is halved, the radius will acquire a factor
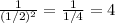
So, the radius will increase by a factor 4, and the Earth will have a larger orbit.