Question

A 900 kg vehicle moves around a curve with an incline of 20\circ∘ at a speed of 12.5 m/s. If the curve has a radius of 50 meters, what normal force [N] will the vehicle experience?

IN NEWTONS

Answer 1

The normal force experienced by the car is approximately 8223.2 N

Step-by-step explanation:

The question relates to banking of road where the centripetal force for the circular motion of the vehicle is provided by the horizontal component of the normal reaction

The mass of the vehicle that moves around the curve, m = 900 kg

The incline of the curve, θ = 20°

The speed with which the vehicle moves around the curve, v = 12.5 m/s

The radius of the curve, R = 50 meters

We have;

`N \cdot sin(\theta) = (m \cdot v^2)/(R)`

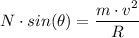
Where;

θ = The angle of inclination of the road = 20°

N = The normal force experienced by the car

m = The mass of the car = 900 kg

v = The velocity with which the car is moving = 12.5 m/s

R = The radius of the curve around which the vehicle moves = 50 m

`\therefore N = (m \cdot v^2)/(R \cdot sin(\theta)) = (900 * (12.5)^2)/(50 * sin(20^(\circ))) = 8223.1998754586828969046217875927`

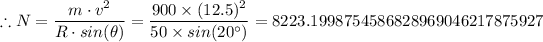
The normal force experienced by the car = N ≈ 8223.2 N.