Question

Find the exact values of the six trigonometric functions of θ if θ is in standard position and the terminal side of θ is in the specified quadrant and satisfies the given condition.

III; parallel to the line
5y − 2x + 1 = 0

Answer 1

So the equation of the line is
`5y -2x + 1 = 0`.

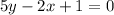
Let's put that in standard form (by solving for y):


`5y -2x + 1 = 0`

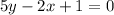
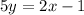
`5y = 2x - 1` ~ we added 2x and subtracted 1 from both sides

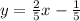
`y = (2)/(5)x - (1)/(5)` ~ divide both sides by 5

So now we have it in the standard form which is
`y = mx + b`.

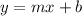
The
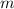
`m` gives us the slope. Recall that slope is rise over run.

So the slope is
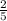
`(2)/(5)`, which means that you could draw a triangle with a rise of 2 and a run of 5.

That's almost enough information to find the trig values, but we still need to know the hypotenuse. Well, thanks to the magic of the Pythagorean Theorem:


`hyp = √(2^2 + 5^2) = √(4+25) = √(29)`

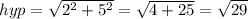
Alright, now that we know all three sides, we can find the values.

The "rise" (vertical) or opposite: 2
The "run" (horozontial) or adjacent: 5
The hypotenuse:
`√(29)`

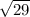
Remember SOHCAHTOA. In order from that mnemonic:

sin(θ) = opposite over hypotenuse =
`(2)/(√(29))`

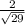
cos(θ) = adjacent over hypotenuse =
`(5)/(√(29))`

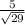
tan(θ) = opposite over adjacent =
`(2)/(5)`

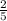
Now the others (cosecant, secant, and cotangent) are just the reciprocals (upside-downs) of the others. Remember that cosecant comes first (since sine comes first in the "usuals".

csc(θ) =
`(√(29))/(2)`

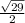
sec(θ) =
`(√(29))/(5)`

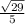
cot(θ) =
`(5)/(2)`

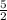
We don't have to 'solve' (approximate) that square root in any of the answers since the problem asked for the exact solution.

Answer 2

5y - 2x + 1 = 0.
5y = 2x-1.

y = 2/5 x - 2/5

this tells us that tan(theta) = 2/5
sin(theta)/sqrt(1-sin^2(theta)) = 2/5
x/sqrt(1-x^2)=2/5
x^2/(1-x^2)=4/25
25x^2=4-4x^2
29x^2=4
x^2=4/29
x = -2/sqrt(29) because quadrant III
cos(x) = sqrt(1-4/29) = -5/sqrt(29)


tan(theta)=2/5
cos(theta)=-5/sqrt(29)
sin(theta)=-2/sqrt(29)
cot(theta)=5/2
sec(theta)=-sqrt(29)/5
csc(theta)=-sqrt(29)/2