Find the approximate area of the parallelogram.

Question

asked Mar 15, 2018 174k views

2 Answers

Rankthefirst · Answer 1 · 2018-03-20T23:29:08+0000

Answer: The area of the given parallelogram is 15 square units.

Step-by-step explanation:

Let ABCD is the parallelogram shown in the graph in which A≡(-2,-1), B≡(-3,3), C≡(1,2) and D≡(2,-2)

Since, AC is the diagonal of the parallelogram,

Thus, by the property of parallelogram,

Area of triangle ABC = Area of triangle ADC

Since, Area of parallelogram ABCD = Area of triangle ABC + Area of triangle ADC

= Area of triangle ABC + Area of triangle ABC

= 2 ( area of triangle ABC )

Since, the area of triangle ABC

=(1)/(2)|-2(3-2)-3(2-(-1))+1(-1-3)|

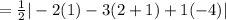
=(1)/(2)|-2(1)-3(2+1)+1(-4)|

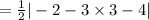
=(1)/(2)|-2-3* 3 -4|

=(1)/(2)|-2-9-4|

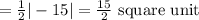
$=(1)/(2)|-15|=(15)/(2)\text{ square unit}$

⇒ Area of parallelogram ABCD =
2* (15)/(2)

=(30)/(2)

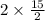
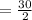
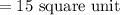
$=15\text{ square unit}$

Hence, The area of the given parallelogram is 15 square units.