Answer: The area of the given parallelogram is 15 square units.
Step-by-step explanation:
Let ABCD is the parallelogram shown in the graph in which A≡(-2,-1), B≡(-3,3), C≡(1,2) and D≡(2,-2)
Since, AC is the diagonal of the parallelogram,
Thus, by the property of parallelogram,
Area of triangle ABC = Area of triangle ADC
Since, Area of parallelogram ABCD = Area of triangle ABC + Area of triangle ADC
= Area of triangle ABC + Area of triangle ABC
= 2 ( area of triangle ABC )
Since, the area of triangle ABC
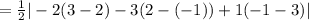
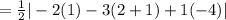
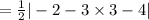
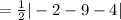
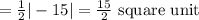
⇒ Area of parallelogram ABCD =
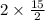
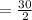
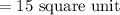
Hence, The area of the given parallelogram is 15 square units.