Question

In △PQR, find the measure of ∡P.

Triangle PQR where angle Q is a right angle. QR measures 33 point 8. PR measures 57 point 6. Measure of angle P is unknown.

30.4°
35.9°
59.6°
54.1°


Is the answer B or something else?

Answer 1

(B) 35.9

Explanation:

Answer 2

∠P = 35.9°

Explanation:

We are given,

A right triangle PQR with ∠Q = 90°, QR = 33.8 and PR = 57.6.

Now, as we know,

In a right triangle, the angles can be written in terms of trigonometric functions.

So, we have,
`\sin P=(Perpendicular)/(Hypotenuse)`

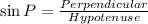
We have that, QR is the perpendicular side and PR is the hypotenuse.

Thus,

`\sin P=(33.8)/(57.6)`

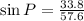
i.e.
`\sin P=0.5868`

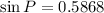
i.e.
`P=\arcsin 0.5868`

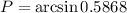
i.e.
`P=35.9`

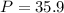
Thus, the measure of ∠P is 35.9°.