Answer:
∠P = 35.9°
Explanation:
We are given,
A right triangle PQR with ∠Q = 90°, QR = 33.8 and PR = 57.6.
Now, as we know,
In a right triangle, the angles can be written in terms of trigonometric functions.
So, we have,

We have that, QR is the perpendicular side and PR is the hypotenuse.
Thus,
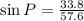
i.e.

i.e.

i.e.

Thus, the measure of ∠P is 35.9°.