Answer:
604800
Explanation:
Given : The ten students in a club are lined up in a row for a group photograph.
To Find: How many different arrangements are possible if the club includes one set of identical triplets wearing matching clothes?
Solution:
The club includes one set of identical triplets wearing matching clothes
So, the remaining students = 10-3 = 7
Now there is an arrangement between these seven students.
Since order has to be maintained .So, we will use permutation
Formula :
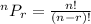
So,
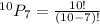
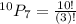
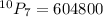
Hence there are 604800 possible arrangements if the club includes one set of identical triplets wearing matching clothes