Question

If F^-1(x) is the inverse of F(x), which statement must be true? Check all that apply.

A. F(F^-1(X))=X
B. F^-1(F(X))=X
C. The range of F^-1(x) is the range of F(x)
D. The range of F^-1(x) is the domain of F(x)
E. The domain of F^-1(x) is the range of F(x)
F. The domain od F^-1(x) is the domain of F(x)

Answer 1

the ones that apply are..... A, B, D, and E

Answer 2

The correct options are:

option: A

`F(F^(-1)(X))=X`

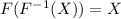
option: B

`F^(-1)(F(X))=X`

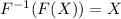
Option: D

The range of F^-1(x) is the domain of F(x)

Option: E

The domain of F^-1(x) is the range of F(x)

Explanation:

We know that for a given function F(X) and it's inverse i.e.
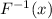`F^(-1)(x)` the composition of both the results in a identity function no matter what the order is such that:

`F(F^(-1)(X))=F^(-1)(F(X))=X`

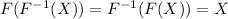
Also, for a inverse of a given function the domain and the range gets interchange.

i.e. the domain of the function becomes the range of it's inverse and the range of the function becomes the domain of it's inverse.