Question

Given the right triangle MLK and PLN below ; PL=15, KN=4 and cos(L)= (4/5). Find the length of KM

Answer 1

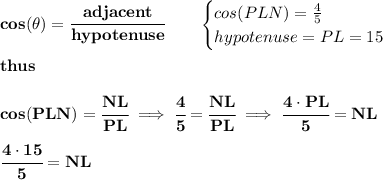
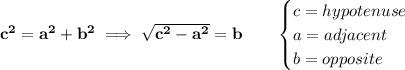for the angle PLN, the hypotenuse PL = 15, the cosine of it is 4/5,
what about the length of NL? well, NL would be the "adjacent" side
of the angle PLN, so, recall your SOH CAH TOA


`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad \qquad % cosine cos(\theta)=\cfrac{adjacent}{hypotenuse} \\ \quad \\ % tangent tan(\theta)=\cfrac{opposite}{adjacent}`

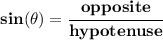
which of those fellows, give us only
the angle
adjacent side
and
hypotenuse?

well, is Ms Cosine, so let's bother her

`\bf cos(\theta)=\cfrac{adjacent}{hypotenuse}\qquad \begin{cases} cos(PLN)=(4)/(5)\\ hypotenuse=PL=15 \end{cases} \\\\ thus \\\\ cos(PLN)=\cfrac{NL}{PL}\implies \cfrac{4}{5}=\cfrac{NL}{PL}\implies \cfrac{4\cdot PL}{5}=NL \\\\ \cfrac{4\cdot 15}{5}=NL`

now, that we know what NL is, what is ML?

notice, the angle MLK is really the same shared angle PLN
so the cosine of that is the same 4/5

so let us use cosine again, now for the bigger triangle though

`\bf cos(\theta)=\cfrac{adjacent}{hypotenuse}\qquad \begin{cases} adjacent=KL=KN+NL\\ cos(MLK)=(4)/(5) \end{cases} \\\\\\ cos(MLK)=\cfrac{KN+NL}{ML}\implies \cfrac{4}{5}=\cfrac{4+NL}{ML}\implies ML=\cfrac{5(4+NL)}{4}`

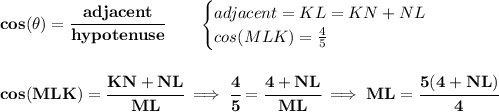
so.. now we know what the sides of KL and ML are,
but what about MK? well
notice, is a right-triangle,
you have the hypotenuse ML,
you also have the adjacent side, KL,

to find the opposite side of MK, simply use the pythagorean theorem


`\bf c^2=a^2+b^2\implies √(c^2-a^2)=b\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite \end{cases}`