Answer:
Givens
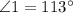
In the image provided we have a pair of parallels lines and a transversal, this setup forms 8 angles which are related in pairs.
Therefore,
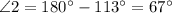 , by supplementary angles defintion.
, by supplementary angles defintion.
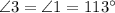 , by corresponding angles definition.
, by corresponding angles definition.
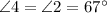 , by supplementary angles.
, by supplementary angles.
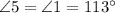 , by alternate exterior angles.
, by alternate exterior angles.
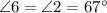 , by alternate exterior angles.
, by alternate exterior angles.
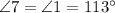 , by vertical angles definition.
, by vertical angles definition.
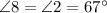 , by vertical angles.
, by vertical angles.
The answer to the second question is 76°, that's the value that makes lines a and b parallel, because that way those angles would be alternate interior angles, which are always congruent when they are formed by a pair of parallels and a transversal.