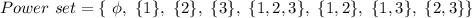Question

The number of subsets that can be created from the set {1, 2, 3} is: 3 6 7 8

Answer 1

6 (1), (2), (3), (1,2), (1,3), and (2,3)

Answer 2

The number of subsets that can be created from the set {1, 2, 3} is:

8

Explanation:

We know that for any set with n elements.

The total number of subsets is given by the formula:

`Total\ number\ of\ subsets=2^n`

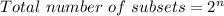
The collection of all the subsets of a set is also known as a Power set.

Here we have a set as: {1,2,3}

i.e. n=3

(There are 3 elements in the set)

Hence, the total number of subsets that can be created by this set will be:

`2^3=2* 2* 2=8`

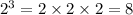
The power set of this set is given by:

`Power\ set=\{\ \phi,\ \{1\},\ \{2\},\ \{3\},\ \{1,2,3\},\ \{1,2\},\ \{1,3\},\ \{2,3\}\}`