Let

be the random variable for the part's diameter, and
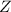
the same variable transformed into one that follows the standard normal distribution. You're looking for the proportion of the parts that lie 2 standard deviations away from the mean, which translates to
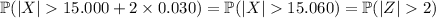
Recall the empirical rule, which says that approximately 95% of a normal distribution falls within 2 standard deviations of the mean, or
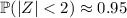
. This means
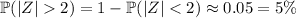
So out of 15000 parts, you should expect about 5% of them, or about 750 parts to be rejected.