Any tangent line to
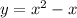
at a point
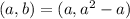
will have slope
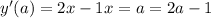
. Such a line has equation
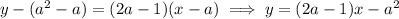
For this (these) line(s) to pass through (2, -3), you must have
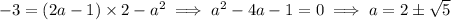
So the two lines in questions are
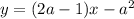
for these values of

.
To show there is no tangent line that passes through (2, 7), you have to show there is no solution for

in
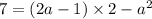
You have
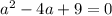
but this has no real solutions, so no such tangent line exists.