Answer:
3, 4, 5
Explanation:
We are given the sets of numbers and we are supposed to find Which set of numbers could represent the lengths of the sides of a right triangle
So, we need to use Pythagoras theorem
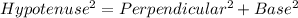
1) 9,10,11
Hypotenuse = 11
So, using Pythagoras theorem
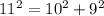
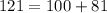
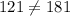
Since the given set does not satisfy the Pythagoras theorem.So, the given set of number could not represent the lengths of the sides of a right triangle.
2)16, 32, 36
Hypotenuse = 36
So, using Pythagoras theorem
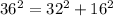

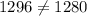
Since the given set does not satisfy the Pythagoras theorem.So, the given set of number could not represent the lengths of the sides of a right triangle.
3)8, 12, 16
Hypotenuse = 36
So, using Pythagoras theorem
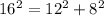

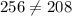
Since the given set does not satisfy the Pythagoras theorem.So, the given set of number could not represent the lengths of the sides of a right triangle.
4)3, 4, 5
Hypotenuse = 5
So, using Pythagoras theorem

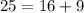
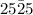
Since the given set satisfy the Pythagoras theorem.So, the given set of number could represent the lengths of the sides of a right triangle.
Hence 3, 4, 5 is the set of numbers could represent the lengths of the sides of a right triangle