Since the question is partial, i will assume 2 scenarios:
- They need to raise 1000 income
- They need to make 1000 as profit
If $1000 as income:
Each ticket costs $15, so
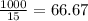 tickets would bring them $1000 income. Fractional ticket is not possible, so rounding gives us 67 tickets as the answer.
tickets would bring them $1000 income. Fractional ticket is not possible, so rounding gives us 67 tickets as the answer.
If $1000 as profit:
Their cost of renting is $700. We know that
 .
.
So,
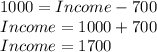 . So, to raise $1700, we need
. So, to raise $1700, we need
 tickets. Fractional ticket is not possible, so rounding gives us 114 tickets as the answer.
tickets. Fractional ticket is not possible, so rounding gives us 114 tickets as the answer.
ANSWER:
If need to raise atleast $1000 as income, they need to sell 67 tickets.
If need to raise atleast $1000 as profit, they need to sell 114 tickets.