Answer:
The number of times one needs to use the completely filled cone to completely fill the cylinder with water is 24.
Step-by-step explanation:
Radius of cylinder = r = 10 cm
Height of cylinder = h = 20 cm
Volume of cylinder= V =
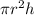 ...(1)
...(1)
Radius of the cone = r' = 5 cm
Height of cone = h' = 10 cm
Volume of cone = V' =
 ...(2)
...(2)
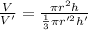
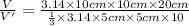

V = 24V'
The number of times one needs to use the completely filled cone to completely fill the cylinder with water is 24.