Question

Synthetic division And the Remainder theorem

One factor of f(x)=4x^3-4x^2-16x+16 is (x – 2). What are all the roots of the function? Use the Remainder Theorem.
A) x = 1, x = 2, or x = 4
B) x = –2, x = 1, or x = 2
C) x = 2, x = 4, or x = 16
D) x = –16, x = 2, or x = 16

Answer 1

The answer to this question is "B.) x = -2, x = 1, or x = 2"

Answer 2

The remainder theorem says that if
`x-c` is a factor of a polynomial
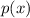
`p(x)`, then the remainder upon dividing
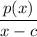
`(p(x))/(x-c)` is 0 so that there exists a lower degree polynomial
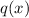
`q(x)` as the quotient:


`(p(x))/(x-c)=q(x)`

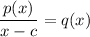
Using the fact that
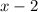
`x-2` is a factor, you can find a quadratic
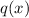
`q(x)` which is easy to factorize further.

Synthetic division yields


`q(x)=4x^2+4x-8`

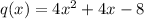
which can be factored further as


`4(x^2+x-2)=4(x+2)(x-1)`

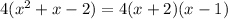
So,


`f(x)=4x^3-4x^2-16x+16=4(x-2)(x+2)(x-1)`

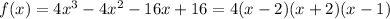
The roots are then
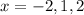
`x=-2,1,2`.