Answer:
Option C.
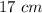
Explanation:
we know that
The Triangle Inequality Theorem, states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
so
Let
c------> the length of the third side
case 1)
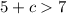
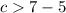
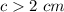
case 2)
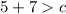
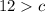 ------> rewrite
------> rewrite
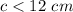
The solution of the third side is the interval------->
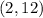
therefore
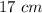 can not be a measure of the third side
can not be a measure of the third side