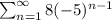Question

Write the sum using summation notation, assuming the suggested pattern continues. 8 - 40 + 200 - 1000 + ...

Answer 1

Each successive term is -5 times the previous one, so the underlying sequence is


`a_n=-5a_(n-1)=(-5)^2a_(n-2)=(-5)^3a_(n-3)=\cdots=(-5)^(n-1)a_1=8(-5)^(n-1)`

The sum can then be written as


`8-40+200-1000+\cdots=\displaystyle\sum_(n=1)^\infty8(-5)^(n-1)`

Answer 2

Explanation:

From the given information, the pattern is as:

8 - 40 + 200 - 1000 + ...

We can see that the successive term is -5 times the previous one, therefore, using this, we can write it in the form of sequence:

`a_(n)=-5a_(n-1)=(-5)^2a_(n-2)=(-5)^3a_(n-3)=....=(-5)^(n-1)a_(1)=8(-5)^(n-1)`.

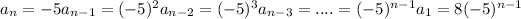Therefore, the sum can be written as:

8 - 40 + 200 - 1000 + ...=
`\sum_(n=1)^(\infty)8(-5)^(n-1)`