Answer:
Required coefficient :coefficient of 1st, 2nd, 3rd and 4th term are 1, 3,3,1 respectively.
Explanation:
Formula for binomial expansion is

We will substitute the values a=a, b=b and n=3 in the formula for binomial expansion we will get
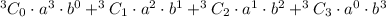
After simplification of the terms we will get

Since,
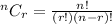
Therefore the required coefficient : coefficients of 1st, 2nd, 3rd and 4th term are 1, 3,3,1 respectively.