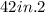Question

The regular hexagon has a radius of 4 in.

What is the approximate area of the hexagon?

24 in.2
42 in.2
48 in.2
84 in.2

Answer 1

`\bf \textit{area of a regular polygon}=\cfrac{1}{2}nR^2\cdot sin\left((360)/(n) \right) \\ \quad \\ \quad \\ \begin{cases} n=\textit{number of sides in the polygon}\\ R=\textit{radius of the polygon} \end{cases}`

so, sides= n= 6
radius = R = 4

`\bf \textit{area of a regular polygon}=\cfrac{1}{2}nR^2\cdot sin\left((360)/(n) \right) \\ \quad \\ \quad \\ \begin{cases} n=\textit{number of sides in the polygon}\\ R=\textit{radius of the polygon} \end{cases} \\ \quad \\ \quad \\ \cfrac{1}{2}6\cdot 4^2\cdot sin\left((360)/(6) \right)\implies \cfrac{1}{2}\cdot 96\cdot sin\left(60^o \right) \\ \quad \\ 48\cdot sin\left(60^o \right)`

Answer 2

we know that

The Area of a Regular Polygon is equal to the formula

`A=\cfrac{1}{2}nr^2\cdot sin\left((360)/(n) \right)`

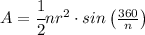
where

n is number of sides in the polygon

r is the radius of the polygon

In this problem

the regular polygon is a hexagon with radius of
`4` in

So

`n=6\\ r=4 in`

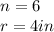
Substitute the value of n and r in the formula above

`A=\cfrac{1}{2}*6*4^2\cdot sin\left((360)/(6) \right)\\ \\A=\cfrac{96}{2}* sin(60) \\ \\ A=(96)/(2) *(√(3))/(2) \\ \\ A=24√(3) \\ \\ A=41.57 in^(2)`

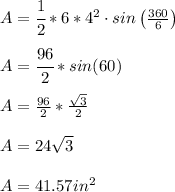
therefore

the answer is the option

`42 in.2`