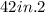we know that
The Area of a Regular Polygon is equal to the formula
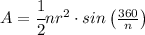
where
n is number of sides in the polygon
r is the radius of the polygon
In this problem
the regular polygon is a hexagon with radius of
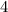 in
in
So
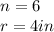
Substitute the value of n and r in the formula above
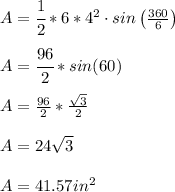
therefore
the answer is the option