Answer:
Find the slope and the y-intercept
Explanation:
To find slope, use the equation
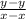 . First, find two points on the line that are near each other and are whole numbers. Then you substitute the points into the equation. So for example, if I had the points (0,0) and (1,2), the substitution would be:
. First, find two points on the line that are near each other and are whole numbers. Then you substitute the points into the equation. So for example, if I had the points (0,0) and (1,2), the substitution would be:
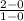
To find the y-intercept, find where the line crosses over the y-axis. Then put in the y value.
If you do not know where to put slope and y-intercept:
y=mx+b
m=slope
b=y-intercept
slope= output/input