Question

What are the vertex and axis of symmetry of the parabola y = x2 – 16x + 63?

A.
vertex: (8, -1); axis of symmetry: x = 8

B.
vertex: (8, 1); axis of symmetry: x = 8

C.
vertex: (-8, 1); axis of symmetry: x = -8

D.
vertex: (-8, -1); axis of symmetry: x = -8

Answer 1

A

Explanation:

Remember that the x-value of the vertex when an equation is given in standard form can be found with the equation
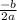`(-b)/(2a)`. So, we can take the coefficients from the equation and plug them in.

`(-b)/(2a) \\(-(-16))/(2(1))\\\\(16)/(2)\\\\8`

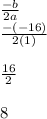
Now we know that the x-value of the vertex is 8. Next, the equation for the y-value is
`c-ah^2`, where h is the x-value of the vertex (8).

`(63)-(1)(8)^2\\63-64\\-1`

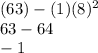
So the vertex is (8,-1).

Finally, the axis of symmetry is the x-value of the vertex, also called h.

Final answer, vertex: (8,-1) and axis of symmetry: x=8

Hope this helps!