Question

A particle moves along a straight line so that its velocity, v ms^-1, at time t seconds is given by v=240+20t-10t^2, for 0≤t≤6.

(i) Find the value of t when the speed of the particle is greatest.
(ii) Find the acceleration of the particle when its speed is zero.

Answer 1

The speed will be greatest on the Vextes of equation

So,

Xv = - b / 2a

As b = 20 and a = -10

Xv = - 20 / 2 . -10

Xv = 20 / 20

Xv = 1 s

Now replace Xv on the equation to find the value of speed

V(t) = 240 + 20t -10t^2

V(Xv) = Vmaximum

V(1) = 240 + 20.(1) - 10.(1)^2

V(1) = 240 + 20 -10

V(1) = 230m/s
____________________


2:

If the speed is zero, then, there isn't acceleration.

Acceleration also is zero.

Answer 2

(i) The speed of the particle is greatest at t=1 and maximum speed is 500 m/s.

(ii) The acceleration of the particle is -100 when its speed is zero.

Explanation:

(i)

We need to find the the time at which time at which the speed of the particle is greatest. It means we need to find the value of t at which velocity function is maximum.

If a function is
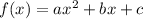`f(x)=ax^2+bx+c`, then the vertex of the function is

`(-(b)/(2a),f(-(b)/(2a)))`

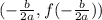
The given velocity function is

`v=240+20t-10t^2`

For 0≤t≤6.

Here, a=-10, b=20 and c=240.

The leading coefficient is negative it means the vertex of the velocity function is the point of maxima.

`-(b)/(2a)=-(20)/(2(-10))\Rightarrow -(20)/(-20)=1`

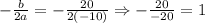
At t=1,

`v=240+20(1)-10(1)^2=250`

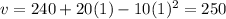
Therefore, the speed of the particle is greatest at t=1 and maximum speed is 500 m/s.

(ii)

Equate the velocity function equal to zero, to find the time at which speed is zero.

`v=0`

`240+20t-10t^2=0`

`10(24+2t-t^2)=0`

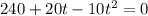
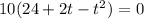
Splitting the middle term we get

`10(24+6t-4t-t^2)=0`

`10(6(4+t)-t(4+t)=0`

`10(6-t)(4+t)=0`

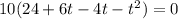
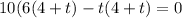
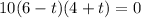
Using zero product property,

`(6-t)=0\Rightarrow t=6`

`4+t=0\Rightarrow t=-4`

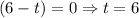
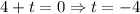
Time can not be negative. So, at t=6 the speed is zero.

Differentiate the velocity function with respect to t.

`a(t)=v'=20(1)-10(2t)`

`a(t)=20-20t`

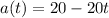
Substitute t=6 in the above function.

`a(t)=20-20(6)`

`a(t)=-100`

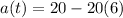
Therefore the acceleration of the particle is -100 when its speed is zero.