Question

Which system of equations does this graph represent?

Answer 1

You just need to list the equations of the two graphs.

y=x^2 + 2
y=x+4

Answer 2

System of the equations will be y = x + 4 and y = x² + 2

Explanation:

The system of equations comprises a parabola and a straight line.

We will form the equation of the line first.

Straight line given in the system passes through two points (2, 6) and (-1, 3).

Since standard for of a straight line is given by y = mx + c

where m = slope and c = y-intercept

So, Slope m =
`(y-y')/(x-x')`

m =
`(6-3)/(2+1)`

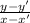
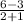
m = 1

And y-intercept c = 4

Therefore, equation of the line will be y = x + 4

For the equation of parabola.

Vertex form of the parabola is represented by,

y = (x - h)² + k

Where (h, k) is the vertex.

Vertex is given in the graph is (0, 2).

So the equation will be y = (x - 0)² + 2

y = x² + 2

Therefore, system of the equations will be y = x + 4 and y = x² + 2