Question

If the digits of a three-digit number are reversed in order, then the sum of the new resulting number and the original number comes out to be 665. The difference of the two numbers is 297. The tens’ digit place is two times the hundreds’ place digit.

Answer 1

xyz - digits of the original number
zyx - digits of the new number

100x +10y + z + 100z +10y + x = 665
101(x+z) +20y = 665
x+z = 5 because the last digit of 665 is 5
(for x+z=15 the last digit of 101*15=15015 is 5 also, but 15015 > 665, it is too much)
101*5 = 505
20y = 665 - 505
20y = 160 /:20
y = 8 //this is tens' place digit
x = y/2 = 4 //because the tens' place digit is two times the hundreds' place digit
z = 5-x = 5-4 = 1

check
481 - the original number
184 - the new number
481 + 184 = 665 ok
481 - 184 = 297 ok
8 = 2 * 4 ok

Answer 2

If
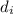
`d_i` is the digit in the
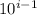
`10^(i-1)`s place (e.g.
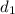
`d_1` is in the ones place,
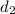
`d_2` is in the tens place, etc), then the original number is


`100d_3+10d_2+d_1`

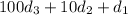
Reversing the digits gives the number


`100d_1+10d_2+d_3`

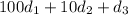
Adding these together results in


`101d_1+20d_2+101d_3=665`

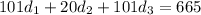
Subtracting (presumably the new number from the original number) yields


`99d_3-99d_1=297`

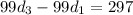
If the tens place contains twice the digit in the hundreds place, then


`d_2=2d_3`

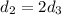
So you have the following system:


`\begin{cases}101d_1+20d_2+101d_3=665\\-99d_1+99d_3=297\\d_2-2d_3=0\end{cases}`

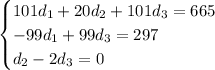
Solving the system should yield
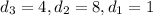
`d_3=4,d_2=8,d_1=1`, so the original number is 481.