Question

The graph of f(x)1/2 = (2.5)^x and its reflection across the x-axis, g(x), are shown.

What is the range of g(x)?

Answer 1

There is a horizontal asymptote at y = 0 so the range is y < 0

Answer 2

The range of g(x) is all real numbers less than 0.

Step-by-step explanation:

Consider the given function:

`f(x)=(1)/(2)(2.5)^x`

The range of a function is the set of all output values.

As it is given that function f(x) reflected across x axis, thus

`g(x)=-f(x)`

`g(x)=-(1)/(2)(2.5)^x`

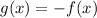
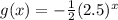
Now consider the provided graph of g(x):

Here, the set of values that are produced by the function g(x) is lies between -∞ to 0.

Therefore, the range of g(x) is all real numbers less than 0.