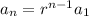Question

What is a quick and easy way to remember explicit and recursive formulas?

Answer 1

I always found derivation to be helpful in remembering. Since this question is tagged as at the middle school level, I assume you've only learned about arithmetic and geometric sequences.

First, remember what these names mean. An arithmetic sequence is a sequence in which consecutive terms are increased by a fixed amount; in other words, it is an additive sequence. If
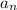
`a_n` is the
`n`th term in the sequence, then the next term
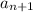
`a_(n+1)` is a fixed constant (the common difference
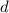
`d`) added to the previous term. As a recursive formula, that's


`a_(n+1)=a_n+d`

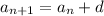
This is the part that's probably easier for you to remember. The explicit formula is easily derived from this definition. Since
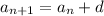
`a_(n+1)=a_n+d`, this means that
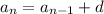
`a_n=a_(n-1)+d`, so you plug this into the recursive formula and end up with


`a_(n+1)=(a_(n-1)+d)+d=a_(n-1)+2d`

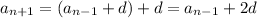
You can continue in this pattern, since every term in the sequence follows this rule:


`a_(n+1)=a_(n-1)+2d`

`a_(n+1)=(a_(n-2)+d)+2d`

`a_(n+1)=a_(n-2)+3d`

`a_(n+1)=(a_(n-3)+d)+3d`

`a_(n+1)=a_(n-3)+4d`

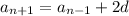
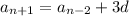
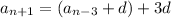
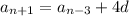
and so on. You start to notice a pattern: the subscript of the earlier term in the sequence (on the right side) and the coefficient of the common difference always add up to
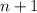
`n+1`. You have, for example,
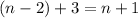
`(n-2)+3=n+1` in the third equation above.

Continuing this pattern, you can write the formula in terms of a known number in the sequence, typically the first one
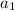
`a_1`. In order for the pattern mentioned above to hold, you would end up with


`a_(n+1)=a_1+nd`

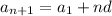
or, shifting the index by one so that the formula gives the
`n`th term explicitly,


`a_n=a_1+(n-1)d`

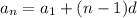
Now, geometric sequences behave similarly, but instead of changing additively, the terms of the sequence are scaled or changed multiplicatively. In other words, there is some fixed common ratio
`r` between terms that scales the next term in the sequence relative to the previous one. As a recursive formula,


`a_(n+1)=ra_n`

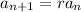
Well, since
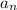
`a_n` is just the term after
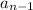
`a_(n-1)` scaled by
`r`, you can write


`a_(n+1)=r(ra_(n-1))=r^2a_(n-1)`

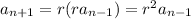
Doing this again and again, you'll see a similar pattern emerge:


`a_(n+1)=r^2a_(n-1)`

`a_(n+1)=r^2(ra_(n-2))`

`a_(n+1)=r^3a_(n-2)`

`a_(n+1)=r^3(ra_(n-3))`

`a_(n+1)=r^4a_(n-3)`

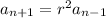
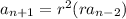
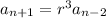
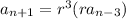
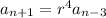
and so on. Notice that the subscript and the exponent of the common ratio both add up to
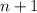
`n+1`. For instance, in the third equation,
`3+(n-2)=n+1`. Extrapolating from this, you can write the explicit rule in terms of the first number in the sequence:


`a_(n+1)=r^na_1`

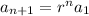
or, to give the formula for
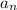
`a_n` explicitly,


`a_n=r^(n-1)a_1`