Question

A continuous function y=f(x) is known to be negative at x=0 and positive at x=1. Why does the equation f(x)=0 have at least one solution between x=0 and x=1?

Answer 1

Because the y values change signs from negative to positive which means the graph had to cross over the x-axis thereby creating a solution.

Answer 2

Givens

It's known that the function is negative at
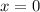`x=0` and positive at
`x=1`.

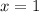To answer this question, we need to use the Intermediate Value Theorem, which states:

• If f(x) is a continuous function on [a, b], then for every k between f(a) and f(b), there exists a value c belongs to (a, b) such that f(c) = k.

Therefore, the function
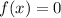`f(x)=0` hast a least one solution between
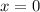`x=0` and
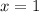`x=1` because the function is continuous in the closed interval [0,1], and based on the intermediate value theorem, if there exist a value inside this interval, then there's at least one solution there.