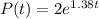Question

The bacterium, cholera, reproduces at an exponential rate which can be modeled through the continuous growth model. If the value for k is 1.38 and we initially start with 2 bacteria, what is the equation for cholera growth, where t is the number of hours?

Answer 1

The continuous growth rate model stipulates that the rate of population change
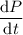
`(\mathrm dP)/(\mathrm dt)` is in proportion with the actual population
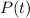
`P(t)` (a function of time
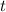
`t`). That is, there is some
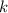
`k` such that


`(\mathrm dP)/(\mathrm dt)=kP`

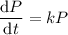
Solving for
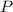
`P`, you get


`(\mathrm dP)/(P)=k\,\mathrm dt\implies \ln|P|=kt+C\implies P=Ce^(kt)`

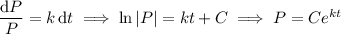
You're given that
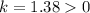
`k=1.38>0`, so the population is increasing. At time
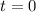
`t=0`, you start with 2 bacteria, so
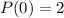
`P(0)=2` and


`2=Ce^(k*0)\implies C=2`

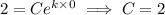
So, the growth equation is


`P(t)=2e^(1.38t)`