Answer:
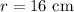
Explanation:
We have been given that in a circle a 45 degree sector has an area of
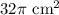 . We are asked to find the radius of our given circle.
. We are asked to find the radius of our given circle.
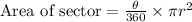
Upon substituting our given values in above formula we will get,
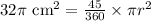
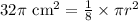
Multiplying both sides of our equation by 8 we will get,
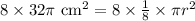
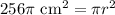
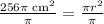

Upon taking square root of both sides of our equation we will get,
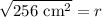
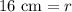
Therefore, the radius of our given circle is 16 cm.