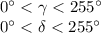Answer:
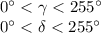
Explanation:
A trapezoid is an irregular type quadrilateral that lacks parallel sides. One of the characteristics of trapezoids is that they have two diagonals and four vertices and when adding their interior angles, the result is 360º. The problem does not give us additional details about the trapezoid or its angles. So, the only equation we can propose is:
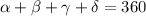
Where:

Are the interior angles of the trapezoid.
Now, let:
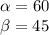
So:
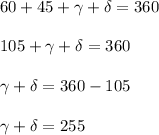
So, based on the information provided, the only thing we can conclude is that the sum of the other angles is 255.
Therefore: