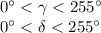Question

A trapezoid has a 60-degree angle and a 45-degree angle. What are the other angles?

Answer 1

`0^(\circ)<\gamma<255^(\circ)\\0^(\circ)<\delta<255^(\circ)`

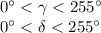
Explanation:

A trapezoid is an irregular type quadrilateral that lacks parallel sides. One of the characteristics of trapezoids is that they have two diagonals and four vertices and when adding their interior angles, the result is 360º. The problem does not give us additional details about the trapezoid or its angles. So, the only equation we can propose is:

`\alpha + \beta +\gamma + \delta=360`

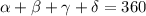
Where:

`\alpha ,\beta ,\gamma ,\delta`

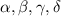
Are the interior angles of the trapezoid.

Now, let:

`\alpha=60\\\beta=45`

So:

`60+45+\gamma+\delta=360\\\\105+\gamma+\delta=360\\\\\gamma+\delta=360-105\\\\\gamma+\delta=255`

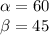
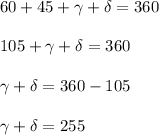
So, based on the information provided, the only thing we can conclude is that the sum of the other angles is 255.

Therefore:

`0^(\circ)<\gamma<255^(\circ)\\0^(\circ)<\delta<255^(\circ)`

Answer 2

A trapezoid is a quadrilateral which means the sum of the angles should be equal to 360 degrees. The other angles therefore should have the sum of 360 - 60 - 45 = 255 degrees. Since we do not have the figure it would be hard to specify the measure of each angle.