Question

What is the equation in point-slope form of a line that passes through the points (7, −8) and (−4, 6) ?

y+6=−1411(x−4)

y+6=−23(x−4)

y−6=−1411(x+4)

y−6=−23(x+4)

Answer 1

(7,-8)(-4,6)
slope = 6 - (-8) / (-4 - 7) = (6 + 8) / -11 = -14/11

point slope : y - y1= m(x - x1)
(-4,6)...x1 = -4 and y1 = 6
now we sub
y - 6 = -14/11(x - (-4) =
y - 6 = -14/11(x + 4) <===

Answer 2

C.
`y-6=-(14)/(11)(x+4)`

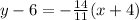
Explanation:

We are given that a line passes through the points (7,-8) and (-4,6).

We have to find the equation in point-slope form of a line .

Slope formula:
`m=(y_2-y_1)/(x_2-x_1)`

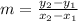
Using the formula

Slope of line=
`m=(6+8)/(-4-7)`

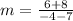
Slope of line=
`m=(14)/(-11)`=
`-(14)/(11)`

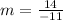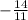
Point-slope form:
`y-y_1=m(x-x_1)`

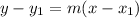
Substitute the values then we get

Equation of line which passing through the point (-4,6) with slope -14/11

`y-6=-(14)/(11)(x+4)`

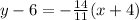
Hence option C is true.