Right away you know that you can't have
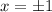
as possible solutions because either of these make the first term's denominator 0, while

also makes the second term's denominator 0.
With this in mind, let's fix
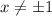
, which allows you to write
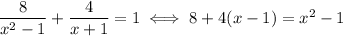
Moving everything to one side, you have

We omitted

from the solution set, so this is an extraneous root and we're left with a solution of

.