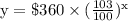Answer:
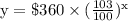
Explanation:
Given: Josiah invests $360 into an account that accrues 3% interest annually.
To Find: Assuming no deposits or withdrawals are made, equation that represents the amount of money in Josiah’s account, y, after x years.
Solution:
Total amount in josiah's account after x years=
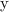
Amount invested in account by Josiah =

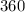
Interest accrued by josiah Annually =
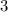 %
%
Total amount of josiah after 1 year =
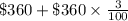
=
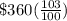
Total amount after 2 years =
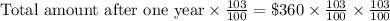
=
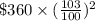
Therefore,
Equation of money in josiah's account after x years