Answer:
75/99.
Explanation:
The infinite geometric sum formula when
 is
is
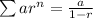
So, we know that
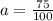 , because it represents the beginning of the number.
, because it represents the beginning of the number.
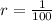 , because the periodic number repeats each two digits.
, because the periodic number repeats each two digits.
Replacing these values, we have
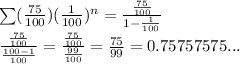
Therefore, the fraction would be 75/99.
If you wanna demonstrate this is true, you just have to divide, then the quotient will be a rational infinite number like the given one 0.757575...