Answer:
0 and 2
Explanation:
We know that the x intercept is the point where the graph intersect the x axis. At this point , the y coordinate is 0. Hence in order to find the x intercepts we have to put y = 0 and solve it for x .
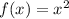
put f(x)=0
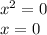
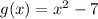
put g(x)=0
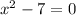
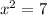
taking square root on both sides we get
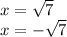
hence in f(x) we have x intercept is one and in g(x) we have two x intercepts.
Part B:

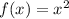
Hence

Hence g(x) is pulled down vertically by 7 units and it will be our transformation.